NetworkLayout

This is the Documentation for NetworkLayout.

All example images on this page are created using Makie.jl and the graphplot recipe from GraphMakie.jl.

using CairoMakie
using NetworkLayout
using GraphMakie, Graphs

Basic Usage & Algorithms

All of the algorithms follow the Layout Interface. Each layout algorithm is represented by a type LayoutAlgorithm <: AbstractLayout. The parameters of each layout can be set with keyword arguments. The LayoutAlgorithm object itself is callable and transforms the adjacency matrix and returns a list of Point{N,T} from GeometryBasics.jl.

alg = LayoutAlgorithm(; p1="foo", p2=:bar)
positions = alg(adj_matrix)

Each of the layouts comes with a lowercase function version:

positions = layoutalgorithm(adj_matrix; p1="foo", b2=:bar)

Instead of using the adjacency matrix you can use AbstractGraph types from Graphs.jl directly.

g = complete_graph(10)
positions = layoutalgorithm(g)

Scalable Force Directed Placement

NetworkLayout.SFDP — Type

SFDP(; kwargs...)(adj_matrix)
sfdp(adj_matrix; kwargs...)

Using the Spring-Electric model suggested by Hu (2005, The Mathematica Journal, pdf).

Forces are calculated as:

    f_attr(i,j) = ‖xi - xj‖ ² / K ,    i<->j
    f_repln(i,j) = -CK² / ‖xi - xj‖ ,  i!=j

Takes adjacency matrix representation of a network and returns coordinates of the nodes.

Keyword Arguments

dim=2, Ptype=Float64: Determines dimension and output type Point{dim,Ptype}.
tol=1.0: Stop if position changes of last step Δp <= tol*K for all nodes
C=0.2, K=1.0: Parameters to tweak forces.
iterations=100: maximum number of iterations
initialpos=Point{dim,Ptype}[]
Provide Vector or Dict of initial positions. All positions will be initialized using random coordinates between [-1,1]. Random positions will be overwritten using the key-val-pairs provided by this argument.
pin=[]: Pin node positions (won't be updated). Can be given as Vector or Dict of node index -> value pairings. Values can be either
- (12, 4.0) : overwrite initial position and pin
- true/false : pin this position
- (true, false, false) : only pin certain coordinates
seed=1: Seed for random initial positions.

source

Example

g = wheel_graph(10)
layout = SFDP(Ptype=Float32, tol=0.01, C=0.2, K=1)
f, ax, p = graphplot(g, layout=layout)
hidedecorations!(ax); hidespines!(ax); ax.aspect = DataAspect(); f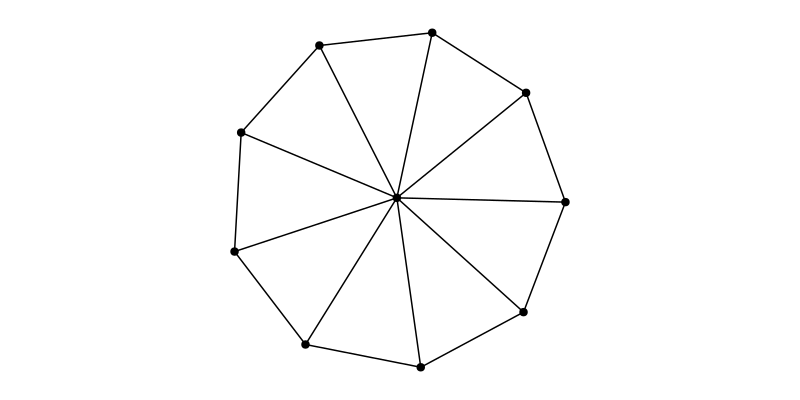

Iterator Example

iterator = LayoutIterator(layout, g)
record(f, "sfdp_animation.mp4", iterator; framerate = 10) do pos
    p[:node_pos][] = pos
    autolimits!(ax)
end

Buchheim Tree Drawing

NetworkLayout.Buchheim — Type

Buchheim(; kwargs...)(adj_matrix)
Buchheim(; kwargs...)(adj_list)
buchheim(adj_matrix; kwargs...)
buchheim(adj_list; kwargs...)

Using the algorithm proposed by Buchheim, Junger and Leipert (2002, doi 10.1007/3-540-36151-0_32).

Takes adjacency matrix or list representation of given tree and returns coordinates of the nodes.

Keyword Arguments

Ptype=Float64: Determines the output type Point{2,Ptype}.
nodesize=Float64[]
Determines the size of each of the node. If network size does not match the length of nodesize fill up with ones or truncate given parameter.

source

Example

adj_matrix = [0 1 1 0 0 0 0 0 0 0;
              0 0 0 0 1 1 0 0 0 0;
              0 0 0 1 0 0 1 0 1 0;
              0 0 0 0 0 0 0 0 0 0;
              0 0 0 0 0 0 0 1 0 1;
              0 0 0 0 0 0 0 0 0 0;
              0 0 0 0 0 0 0 0 0 0;
              0 0 0 0 0 0 0 0 0 0;
              0 0 0 0 0 0 0 0 0 0;
              0 0 0 0 0 0 0 0 0 0]
g = SimpleDiGraph(adj_matrix)
layout = Buchheim()
f, ax, p = graphplot(g, layout=layout)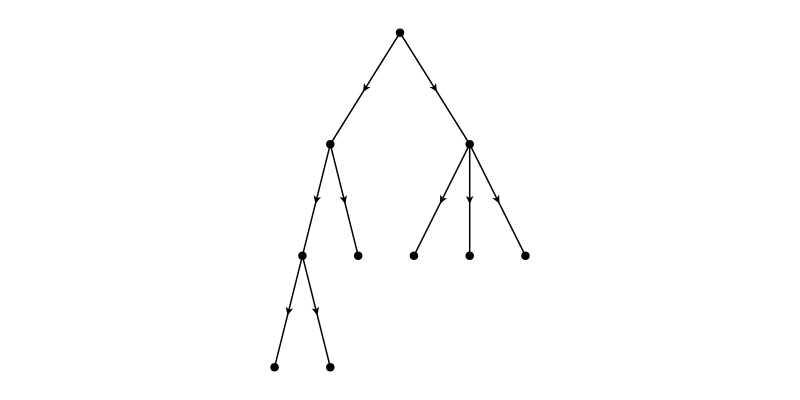

Spring/Repulsion Model

NetworkLayout.Spring — Type

Spring(; kwargs...)(adj_matrix)
spring(adj_matrix; kwargs...)

Use the spring/repulsion model of Fruchterman and Reingold (1991, doi 10.1002/spe.4380211102) with

Attractive force: f_a(d) = d^2 / k
Repulsive force: f_r(d) = -k^2 / d

where d is distance between two vertices and the optimal distance between vertices k is defined as C * sqrt( area / num_vertices ) where C is a parameter we can adjust

Takes adjacency matrix representation of a network and returns coordinates of the nodes.

Keyword Arguments

dim=2, Ptype=Float64: Determines dimension and output type Point{dim,Ptype}.
C=2.0: Constant to fiddle with density of resulting layout
iterations=100: maximum number of iterations
initialtemp=2.0: Initial "temperature", controls movement per iteration
initialpos=Point{dim,Ptype}[]
Provide Vector or Dict of initial positions. All positions will be initialized using random coordinates between [-1,1]. Random positions will be overwritten using the key-val-pairs provided by this argument.
pin=[]: Pin node positions (won't be updated). Can be given as Vector or Dict of node index -> value pairings. Values can be either
- (12, 4.0) : overwrite initial position and pin
- true/false : pin this position
- (true, false, false) : only pin certain coordinates
seed=1: Seed for random initial positions.

source

Example

g = smallgraph(:cubical)
layout = Spring(Ptype=Float32)
f, ax, p = graphplot(g, layout=layout)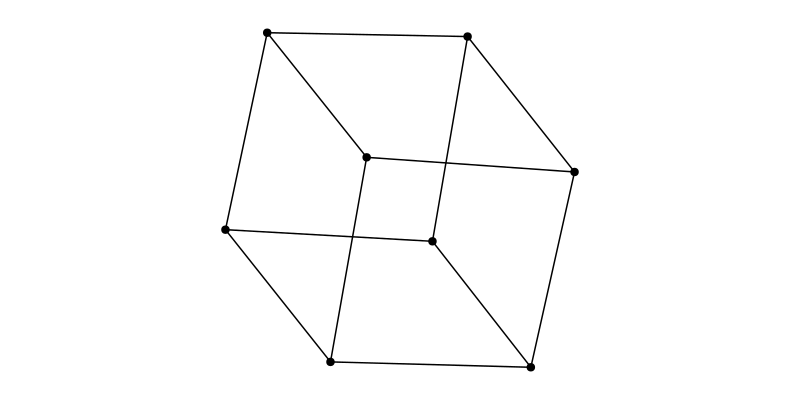

Iterator Example

iterator = LayoutIterator(layout, g)
record(f, "spring_animation.mp4", iterator; framerate = 10) do pos
    p[:node_pos][] = pos
    autolimits!(ax)
end

Stress Majorization

NetworkLayout.Stress — Type

Stress(; kwargs...)(adj_matrix)
stress(adj_matrix; kwargs...)

Compute graph layout using stress majorization. Takes adjacency matrix representation of a network and returns coordinates of the nodes.

The main equation to solve is (8) in Gansner, Koren and North (2005, doi 10.1007/978-3-540-31843-9_25).

Inputs:

adj_matrix: Matrix of pairwise distances.

Keyword Arguments

dim=2, Ptype=Float64: Determines dimension and output type Point{dim,Ptype}.
iterations=:auto: maximum number of iterations (:auto means 400*N^2 where N are the number of vertices)
abstols=0
Absolute tolerance for convergence of stress. The iterations terminate if the difference between two successive stresses is less than abstol.
reltols=10e-6
Relative tolerance for convergence of stress. The iterations terminate if the difference between two successive stresses relative to the current stress is less than reltol.
abstolx=10e-6
Absolute tolerance for convergence of layout. The iterations terminate if the Frobenius norm of two successive layouts is less than abstolx.
weights=Array{Float64}(undef, 0, 0)
Matrix of weights. If empty (i.e. not specified), defaults to weights[i,j] = δ[i,j]^-2 if δ[i,j] is nonzero, or 0 otherwise.
initialpos=Point{dim,Ptype}[]
Provide Vector or Dict of initial positions. All positions will be initialized using random coordinates from normal distribution. Random positions will be overwritten using the key-val-pairs provided by this argument.
pin=[]: Pin node positions (won't be updated). Can be given as Vector or Dict of node index -> value pairings. Values can be either
- (12, 4.0) : overwrite initial position and pin
- true/false : pin this position
- (true, false, false) : only pin certain coordinates
seed=1: Seed for random initial positions.

source

Example

g = SimpleGraph(936)
for l in eachline(joinpath(@__DIR__,"..","..","test","jagmesh1.mtx"))
    s = split(l, " ")
    src, dst = parse(Int, s[1]), parse(Int, s[2])
    src != dst && add_edge!(g, src, dst)
end

layout = Stress(Ptype=Float32)
f, ax, p = graphplot(g; layout=layout, node_size=3, edge_width=1)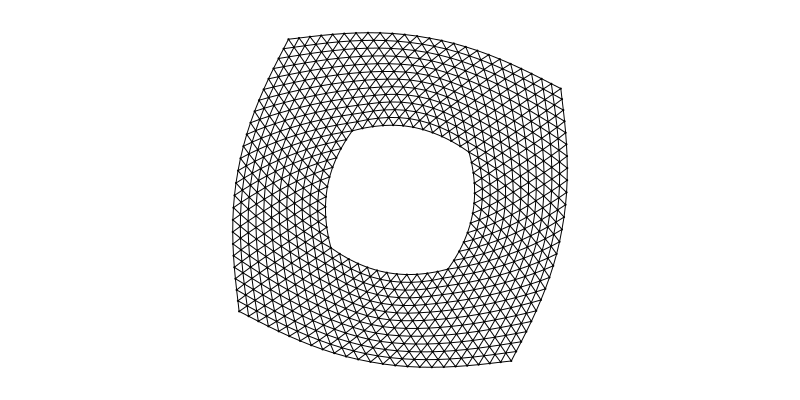

Iterator Example

iterator = LayoutIterator(layout, g)
record(f, "stress_animation.mp4", iterator; framerate = 7) do pos
    p[:node_pos][] = pos
    autolimits!(ax)
end

Shell/Circular Layout

NetworkLayout.Shell — Type

Shell(; kwargs...)(adj_matrix)
shell(adj_matrix; kwargs...)

Position nodes in concentric circles. Without further arguments all nodes will be placed on a circle with radius 1.0. Specify placement of nodes using the nlist argument.

Takes adjacency matrix representation of a network and returns coordinates of the nodes.

Keyword Arguments

Ptype=Float64: Determines the output type Point{2,Ptype}.
nlist=Vector{Int}[]
Vector of Vector of node indices. Tells the algorithm, which nodes to place on which shell from inner to outer. Nodes which are not present in this list will be place on additional outermost shell.

This function started as a copy from IainNZ's GraphLayout.jl

source

g = smallgraph(:petersen)
layout = Shell(nlist=[6:10,])
f, ax, p = graphplot(g, layout=layout)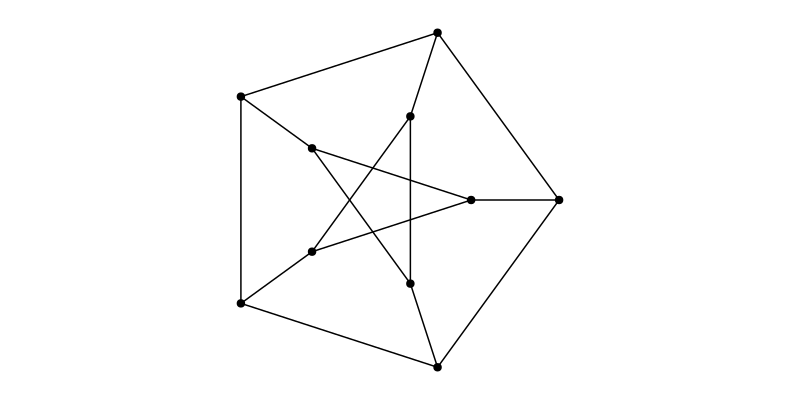

SquareGrid Layout

NetworkLayout.SquareGrid — Type

SquareGrid(; kwargs...)(adj_matrix)
squaregrid(adj_matrix; kwargs...)

Position nodes on a 2 dimensional rectagular grid. The nodes are placed in order from upper left to lower right. To skip positions see skip argument.

Takes adjacency matrix representation of a network and returns coordinates of the nodes.

Keyword Arguments

Ptype=Float64: Determines the output type Point{2,Ptype}
cols=:auto: Columns of the grid, the rows are determined automatic. If :auto the layout will be square-ish.
dx=Ptype(1), dy=Ptype(-1): Ofsets between rows/cols.
skip=Tuple{Int,Int}[]: Specify positions to skip when placing nodes. skip=[(i,j)] means to keep the position in the i-th row and j-th column empty.

source

g = Grid((12,4))
layout = SquareGrid(cols=12)
f, ax, p = graphplot(g, layout=layout, nlabels=repr.(1:nv(g)), nlabels_textsize=10, nlabels_distance=5)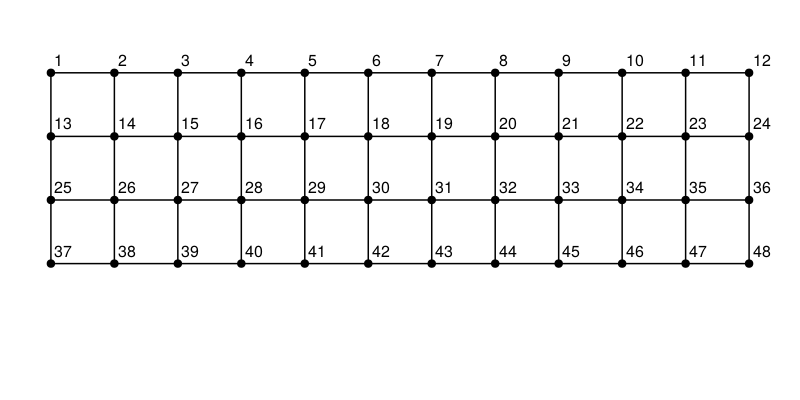

Spectral Layout

NetworkLayout.Spectral — Type

Spectral(; kwargs...)(adj_matrix)
spectral(adj_matrix; kwargs...)

This algorithm uses the technique of Spectral Graph Drawing. For reference see Koren (2003, doi 10.1007/3-540-45071-8_50).

Takes adjacency matrix representation of a network and returns coordinates of the nodes.

Keyword Arguments

dim=3, Ptype=Float64: Determines dimension and output type Point{dim,Ptype}.
nodeweights=Float64[]: Vector of weights. If network size does not match the length of nodesize use ones instead.

source

g = watts_strogatz(1000, 5, 0.03; seed=5)
layout = Spectral(dim=2)
f, ax, p = graphplot(g, layout=layout, node_size=0.0, edge_width=1.0)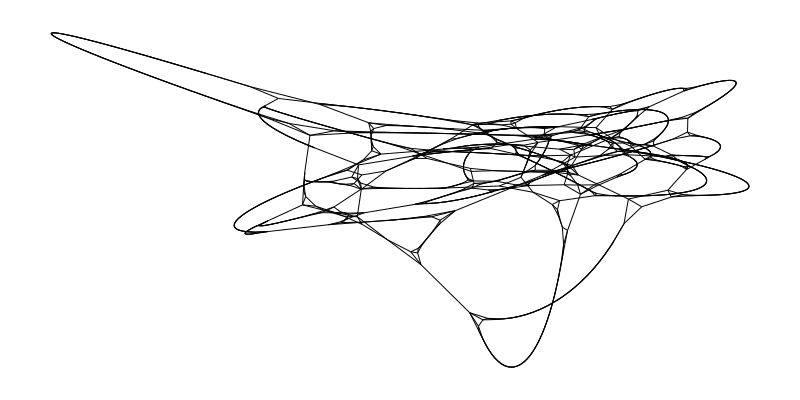

layout = Spectral()
f, ax, p = graphplot(g, layout=layout, node_size=0.0, edge_width=1.0)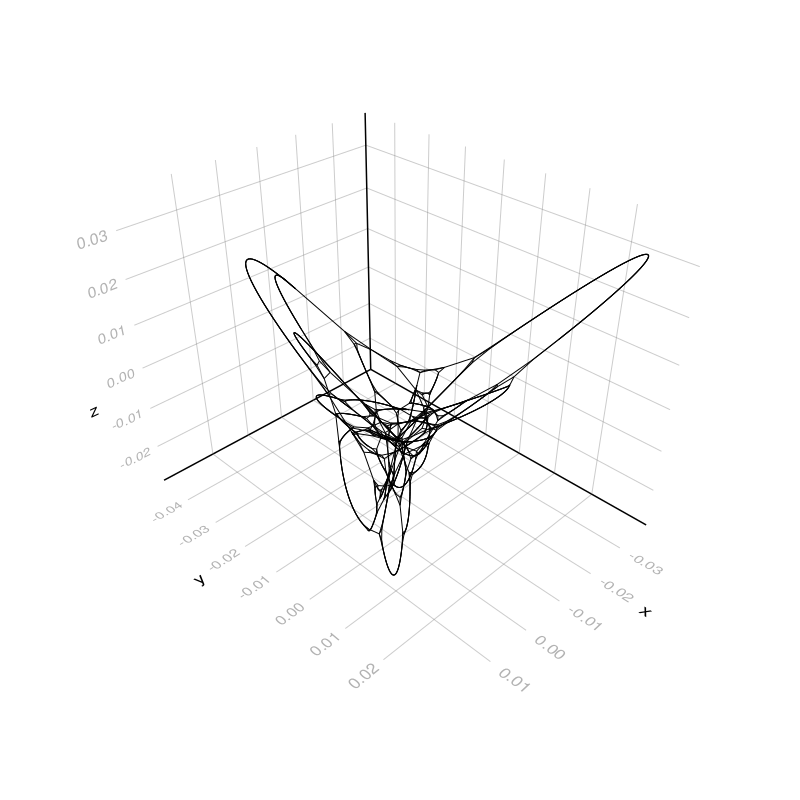

`pin` Positions in Interative Layouts

Sometimes it is desired to fix the positions of a few nodes while arranging the rest "naturally" around them. The iterative layouts Stress, Spring and SFDP allow to pin nodes to certain positions, i.e. those node will stay fixed during the iteration.

g = SimpleGraph(vcat(hcat(zeros(4,4), ones(4,4)), hcat(ones(4,4), zeros(4,4))))

The keyword argument pin takes a Vector or a Dict of key - value pairs. The key has to be the index of the node. The value can take three forms:

idx => Point2(x,y) or idx => (x,y) overwrites the initial position of that vertex and pins it there,
idx => true/false pins or unpins the vertex, position is taken from initialpos-keyword argument or random,
idx => (false, true) allows for fine control over which coordinate to pin.

initialpos = Dict(1=>Point2f(-1,0.5),
                  3=>Point2f(1,0),
                  4=>Point2f(1,0))
pin = Dict(1=>true,
           2=>(-1,-0.5),
           3=>(true, false),
           4=>(true, false))

Example animation on how those keyword arguments effect different iterative layouts:

springl = Spring(;initialpos, pin, seed=11) #2
sfdpl   = SFDP(;initialpos, pin, tol=0.0)
stressl = Stress(;initialpos, pin, reltols=0.0, abstolx=0.0, iterations=100)

f = Figure(resolution=(1200,500))
ax1 = f[1,1] = Axis(f; title="Spring")
ax2 = f[1,2] = Axis(f; title="SFDP")
ax3 = f[1,3] = Axis(f; title="Stress")

for ax in [ax1, ax2, ax3]
    xlims!(ax,-2,2); ylims!(ax,-1.4,1.4); vlines!(ax, 1; color=:red); hidespines!(ax); hidedecorations!(ax)
end

node_color = vcat(:green, :green, :red, :red, [:black for _ in 1:4])
node_size = vcat([40 for _ in 1:4], [20 for _ in 1:4])
nlabels = vcat("1", "2", "3", "4", ["" for _ in 1:4])
nlabels_align = (:center, :center)
nlabels_color = :white
p1 = graphplot!(ax1, g; layout=springl, node_color, node_size, nlabels, nlabels_align, nlabels_color)
p2 = graphplot!(ax2, g; layout=sfdpl, node_color, node_size, nlabels, nlabels_align, nlabels_color)
p3 = graphplot!(ax3, g; layout=stressl, node_color, node_size, nlabels, nlabels_align, nlabels_color)

iterators = [LayoutIterator(l, g) for l in (springl, sfdpl, stressl)]
record(f, "pin_animation.mp4", zip(iterators...); framerate = 10) do (pos1, pos2, pos3)
    p1[:node_pos][] = pos1
    p2[:node_pos][] = pos2
    p3[:node_pos][] = pos3
end